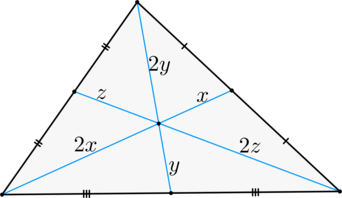
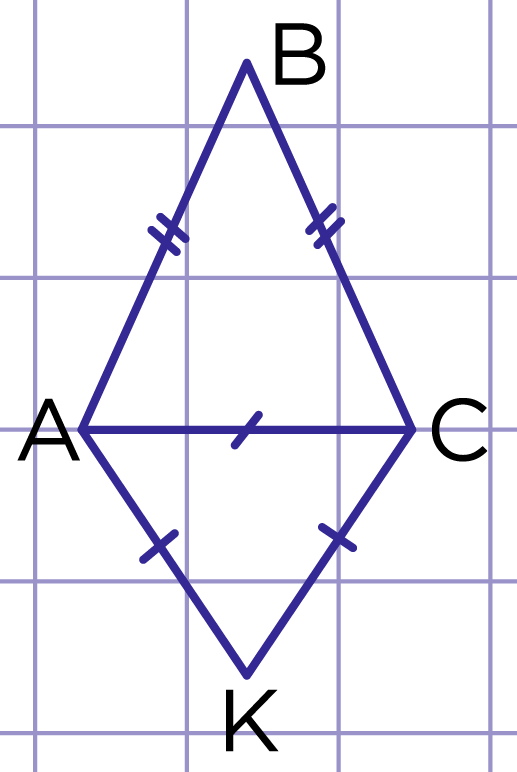
Равнобедренный треугольник отношение медиан

Регистрация Вход. Ответы Mail.

Равнобедренные и равносторонние треугольники

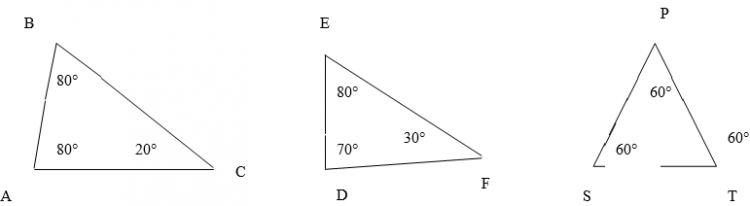
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Против большей стороны находится больший угол; против меньшего угла находится меньшая сторона. Отсюда следует, что если:. Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. Площадь треугольника равна квадратному корню из произведения его полупериметра на разности полупериметра и каждой из его сторон.

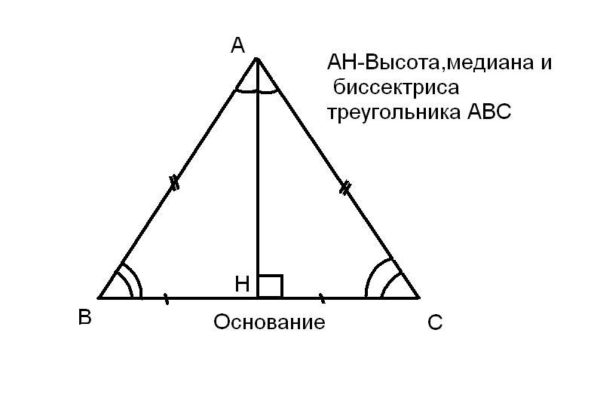
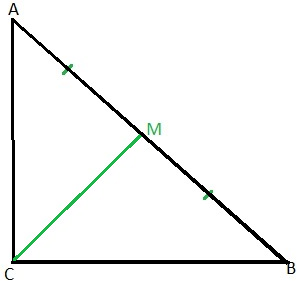
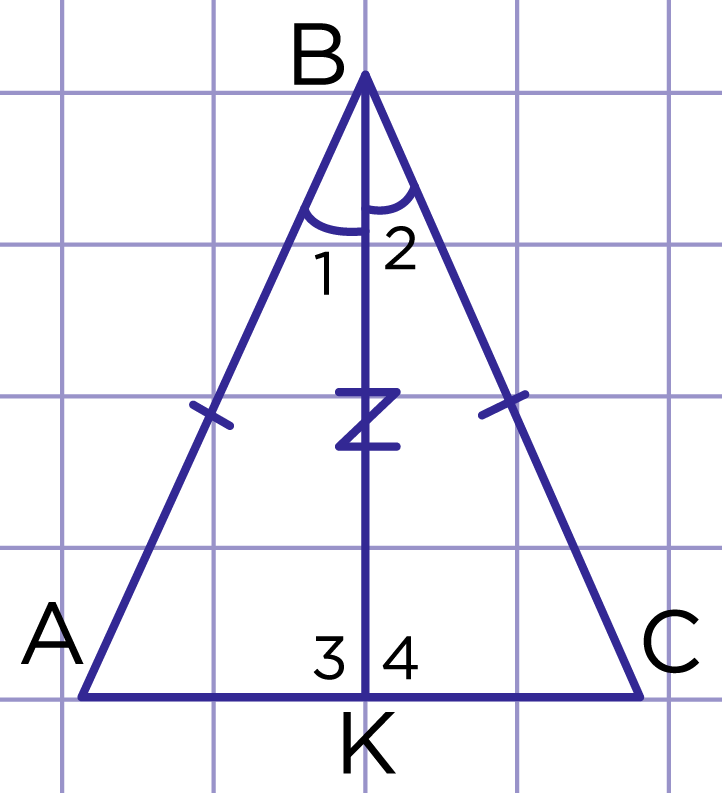
Полные уроки. Эти стороны называются боковыми , а третья сторона — основанием. Свойства равнобедренного треугольника. По первому признаку эти треугольники равны. Отсюда следует Файл Теорема доказана.

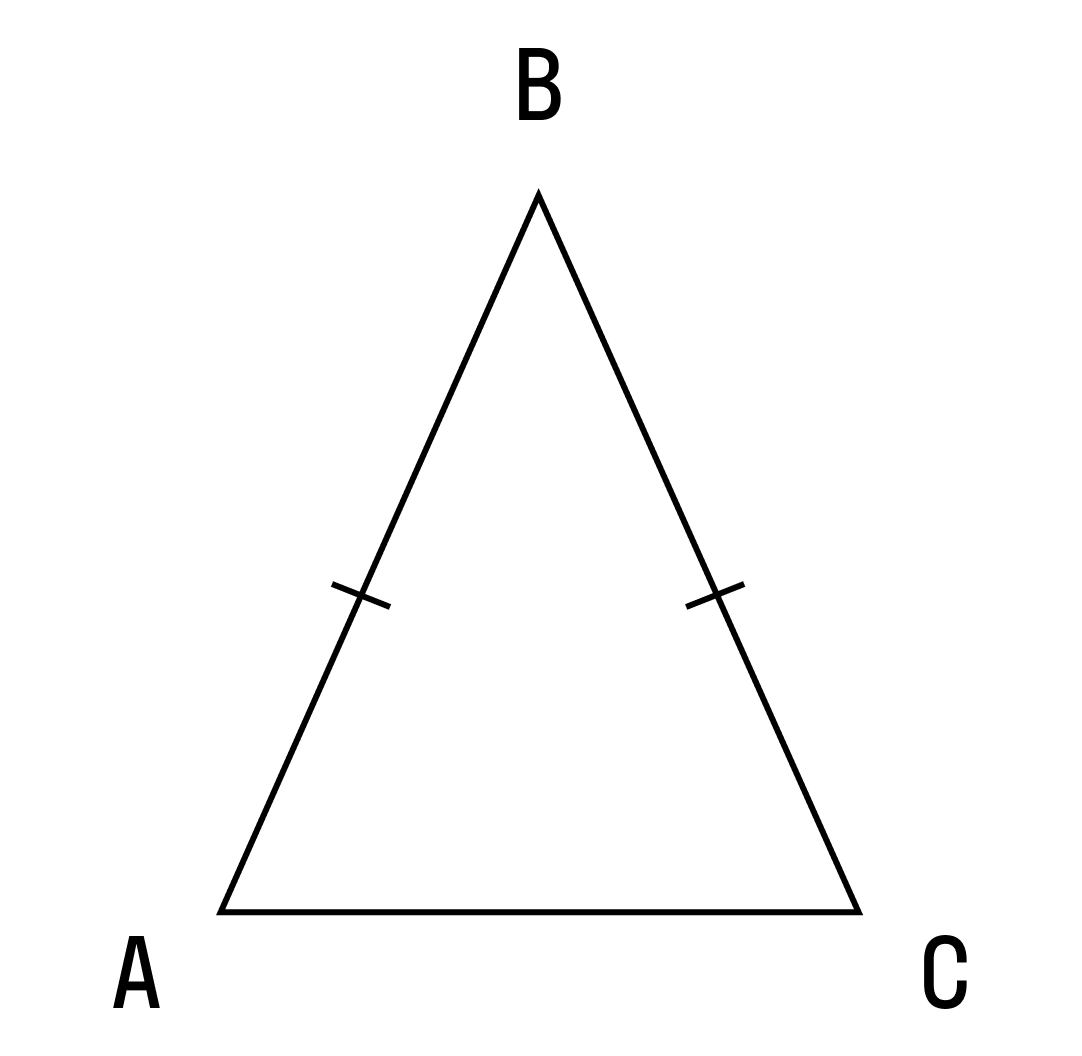
Равнобедренный треугольник — треугольник , в котором две стороны имеют равную длину. Боковыми называются равные стороны, а третья сторона — основанием. Каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно [1]. Угол, образованный боковыми сторонами, называется вершинным углом , а углы, одной из сторон которых является основание, называются углами при основании [1].